希尔排序

发表于 | 分类于 ， | | 阅读次数:

介绍

希尔排序是一种基于插入排序的快速的排序算法。插入排序对于大规模的乱序数组效率很慢，因为它只会交换相邻的元素，因此元素只能一点一点地从数组的一端移动到另一端。希尔排序为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序数组排序。

希尔排序的思想是使数组中任意间隔为h的元素都是有序的，这样的数组称为h有序数组。在进行排序时，如果h很大，就能将元素移动到很远的地方，为实现更小的h有序创造方便。用这种方式，对于任意以1结尾的h序列，都能将数组排序。一个h有序数组即一个由h个有序子数组组成的数组：

希尔排序

实现希尔排序的一种方法是对于每个h，用插入排序将h个子数组独立地排序。但因为子数组是相互独立地，一个更简单地方法是在h-子数组中将每个元素交换到比它大的元素之前去，只需要在插入排序的代码中将移动元素的距离由1改为h即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void shellSort(Comparable[] a){
    //将a[]按升序排列
    int N = a.length;
    int h = 1;
    while(h < N/3){
      h = 3*h + 1;//1, 4, 13, 40, 121, 364...
    }
    while(h >= 1){
      	//将数组变为h有序
      	for(int i = h; i < N; i++){
       	 	//将a[i]插入到a[i-h],a[i-2*h],a[i-3*h]...之中
        	for(int j = i; j > h && less(a[j],a[j-h]); j -= h){
         		 exch(a,j,j-h);
       		 }
      	}
      	h = h/3;
    }
}

说明：

  • 上面算法使用了序列1/2（3^k-1），从N/3开始递减至1，这个序列称为递增序列。
  • 希尔排序更高效的原因是它权衡了子数组的规模和有序性。子数组规模小，部分有序，这两种情况很适合插入排序。
  • 希尔排序与插入排序对比，希尔排序可以用于大型数组。
  • 上面算法的性能，运行时间达不到平方级别（结论）。

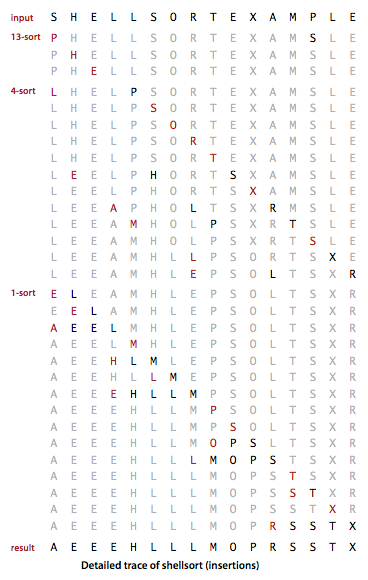
希尔排序的轨迹：