堆排序

发表于 | 分类于 ， | | 阅读次数:

介绍

堆排序可以分为两个阶段。在堆的构造阶段中，我们将原始数组重新组织安排进一个堆中；然后在下沉排序阶段，我们从堆中按递减顺序取出所有元素并得到排序结果。在排序中将直接使用swim（）和sink（）操作，这样在排序时就可以将需要排序的数组本身作为堆，因此不需要任何额外空间。

堆的构造

由N个给定的元素构造一个堆，我们可以在NlogN成正比的时间内完成这项任务，只需要从左至右遍历数组，用swim（）保证扫描指针左侧的所有元素已经是一颗堆有序的完全树即可，就像连续向优先队列中插入元素一样。

另一个更聪明高效的方法是从右至左用sink（）函数构造子堆。数组的每个位置都已经是一个子堆的根结点了，sink（）对于这些子堆也适用。如果一个结点的两个子结点都已经是堆了，那么在该结点上调用sink（）可以将它们变成一个堆。这个过程会递归地建立起堆的秩序。堆的构造和下沉排序图：

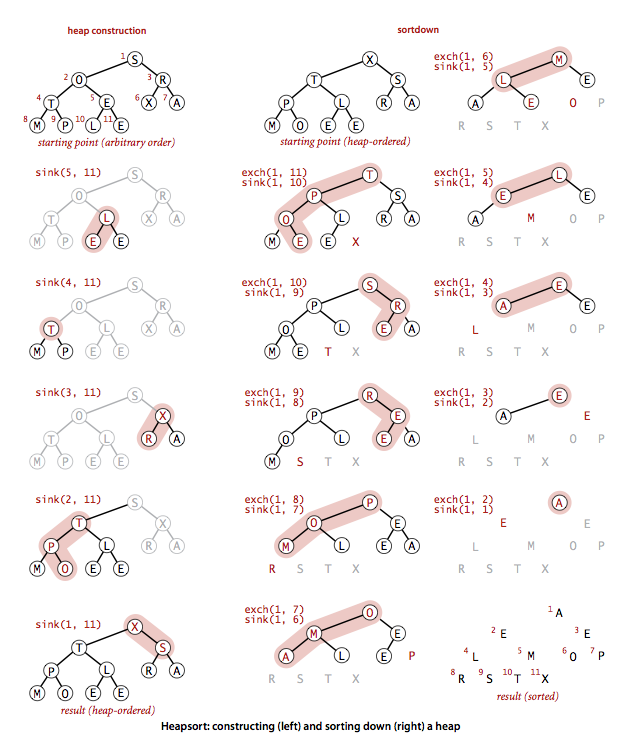
说明：用下沉操作由N个元素构造堆只需少于2N次比较以及少于N次交换。

  • 证明：例如构造一个127个元素的堆，我们会处理32个大小为3的堆，16个大小为7的堆，8个大小为15的堆，4个大小为31的堆，2个大小为63的堆和1个大小为127的堆，因此最坏情况下需要32 1 + 16 2 + 8 3 + 4 4 + 2 5 + 1 6 = 120次交换，以及两倍的比较。

堆排序

下沉排序

主要思想：将堆中的最大元素删除，然后放入堆缩小后数组中空出来的位置。这个过程和选择排序类似（按照降序取出所有元素），但所需的比较要少得多，因为对提供了一种从未排序部分找到最大元素的有效方法。

这段代码完整实现了这些思想，也是经典的堆排序算法。用sink（）方法将a[1]到a[N]的元素排序。for循环构造了堆，然后while循环将最大的元素a[1]和a[N]交换并修复了堆，如此重复直到堆变空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class Heap {    
    private Heap() { }
    public static void sort(Comparable[] pq) {
        int n = pq.length;
      	//构造堆
        for (int k = n/2; k >= 1; k--) {
          	sink(pq, k, n);
        } 
      	//下沉排序中销毁堆
        while (n > 1) {
            exch(pq, 1, n--);
            sink(pq, 1, n);
        }
    }

    private static void sink(Comparable[] pq, int k, int n) {
        while (2*k <= n) {
            int j = 2*k;
            if (j < n && less(pq, j, j+1)) { j++; }
            if (!less(pq, k, j)) { break; }
            exch(pq, k, j);
            k = j;
        }
    }

    private static boolean less(Comparable[] pq, int i, int j) {
        return pq[i-1].compareTo(pq[j-1]) < 0;
    }

    private static void exch(Object[] pq, int i, int j) {
        Object swap = pq[i-1];
        pq[i-1] = pq[j-1];
        pq[j-1] = swap;
    }

    private static void show(Comparable[] a) {
        for (int i = 0; i < a.length; i++) {
            StdOut.println(a[i]);
        }
    }
  
    public static void main(String[] args) {
        String[] a = StdIn.readAllStrings();
        Heap.sort(a);
        show(a);
    }
}

说明：将N个元素排序，堆排序只需少于（2NlgN+2N）次比较（以及一半次数的交换）。

  • 证明：2N来自于堆的构造，2NlgN项来自于每次下沉操作最大可能需要2lgN次比较。

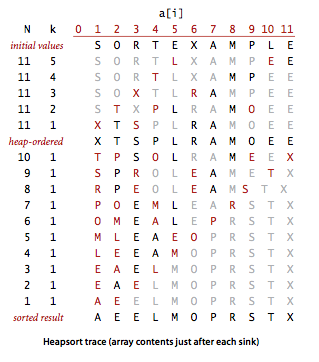
堆排序的轨迹（每次下沉后的数组内容）：

先下沉后上浮

大多数在下沉排序期间重新插入堆的元素会被直接加入到堆底，所以我们正好可以通过免去检查元素是否到达正确的位置来节省时间。在下沉重总是直接提升较大的子结点直至到达堆底，然后使元素上浮到正确的位置。这个想法几乎可以将比较次数减少一半，接近了归并排序所需的比较次数。这种方法需要额外的空间，因此在实际应用中只有当比较操作代价较高时才有用，例如：当为我们在将字符串或者其他键值较长类型的元素进行排序时。

总结

堆排序在排序复杂性的研究中有着重要的地位，因为它是我们所知的唯一能够同时最优地利用空间和时间的方法，在最坏的情况下它也能保证使用~2NlgN次比较和恒定的额外空间。在空间十分紧张的时候（例如嵌入式系统或低成本的移动设备中）很流行。但现代系统的许多应用中很少使用它，因为它无法利用缓存。数组元素很少和相邻的其他元素进行比较，因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法，如快速排序、归并排序，甚至是希尔排序。